Service life planning and service life prediction is today ruled by the ISO 15686 standard. This standard can guide user to find out the Reference Service Life (RSL) of components and materials from both laboratory aging tests and field exposures. In particular, during last years researches on durability of building materials gave considerable results on building materials behavior during their service life, but there is still a lot of work to be done on methods for predicting the Estimated Service Life (ESL) of components or materials in real projects.
The transition from RSL to ESL can be done, according to the ISO 15686, in three different ways: a) factor method, b) engineering methods and c) stochastic methods. During the last years a lot of work has been done in order to evolve factor method to an engineering method by using probabilistic input data. The main reason of this work is that researchers want to have a method that is easy to be used like the factor method and that better follows the uncertainty of input data.
An example (probably the first one) of factor method with PDF as input can be found in Moser, K., Towards the practical evaluation of service life - illustrative application of the probabilistic approach. 8DBMC International Conference on Durability of Building Materials and Components, 30 May-3 June 1999, Vancouver, Canada
Another example is in Re Cecconi, Engineering method for service life planning: the evolved factor method, proceedings of the CIB World Building Congress 2004, Toronto 2-7 May 2004
This software tool for service life planning based on the factor method uses Montecarlo technique to propagate input data uncertainty.
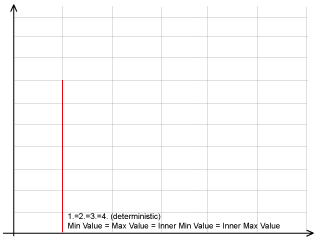
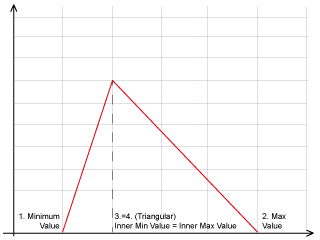
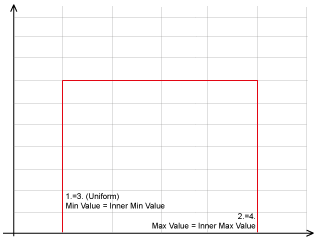
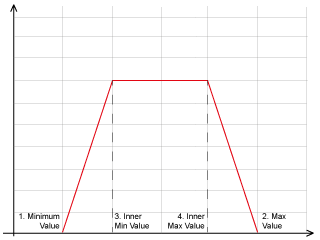
In particular, statistical description of every factor of the method is given by four values:
1. the minimum value,
2. the maximum value,
3. the inner minimum,
4. the inner maximum.
Using these four numbers it is possible to describe different types of PDF as shown in the pictures. Moreover, this kind of description seems to be easier to be used in common practice than other based on the mean and variance of the Gaussian PDF.



